Technical interviews are a common part of the hiring process for software engineering roles. During these interviews, candidates are evaluated on their coding skills, problem-solving abilities, and technical knowledge. The interview format can vary, but coding questions are a key component.
Sometimes you may sit and solve 1000+ Leetcode problems and still get stuck at some coding problems. The main problem is that candidates are having trouble understanding generic patterns. It is like a template that you can use to solve multiple questions.
In this article, we will walk you through some of the most asked coding interview question patterns with examples so that next time you get a clear idea when doing a question.
So let’s get started!
Sliding Window
The Sliding Window pattern is a technique used to work with a specific range of elements within an array or linked list. It’s handy for solving tasks like finding the longest subarray with certain characteristics, such as the longest sub-array problem.
Here’s how it works: You start with the first element and create a “window” of elements. This window shifts one step to the right at a time, and its size changes to match the problem you’re tackling. The window can stay the same size or expand and contract depending on what you need to achieve.

Here’s a basic outline of how the sliding window technique works:
- Initialize Pointers: Set up two pointers, usually representing the start and end of the window, at the beginning of the array.
- Adjust Window: Slide the window to the right by moving the end pointer. This represents including more elements in the window.
- Check Condition: Check if the current window satisfies a given condition or constraint. If it does, you can update your solution or perform other necessary actions.
- Adjust Window Further: If the condition is not satisfied, slide the window further to the right by moving the start pointer. This represents excluding elements from the window.
- Repeat: Continue sliding and adjusting the window until the entire array is covered or a solution is met.
Two pointer approach
These types of problems mostly deal with sorted lists (arrays or linked lists), and the goal is to find a set of elements that fulfil certain conditions. It involves using two pointers that traverse the array or list from different positions or directions to achieve a condition.

Here is the basic outline for the Two pointer approach
- Initialization: Start with two pointers, usually set to different positions in the array or list.
- Traverse or Move: Depending on the problem, you move the pointers in specific ways. For example, you might move one pointer forward while the other moves backwards, or you might both move in the same direction.
- Comparison or Operation: At each step, you compare the elements pointed to by the two pointers or perform a specific operation based on the problem’s requirements.
- Adjustment of Pointers: Based on the comparison or operation, you might adjust the positions of the pointers. You can move both pointers, just one, or neither, depending on the situation.
- Repeat: Continue this process until the pointers meet, cross, or reach a certain condition, depending on the problem’s constraints.
Breadth-First Search
This approach draws inspiration from the Breadth First Search (BFS) algorithm used to traverse trees. It employs a queue to manage nodes at each level before progressing to the subsequent level. Any problem requiring a level-by-level traversal of a tree can be effectively tackled using this strategy.
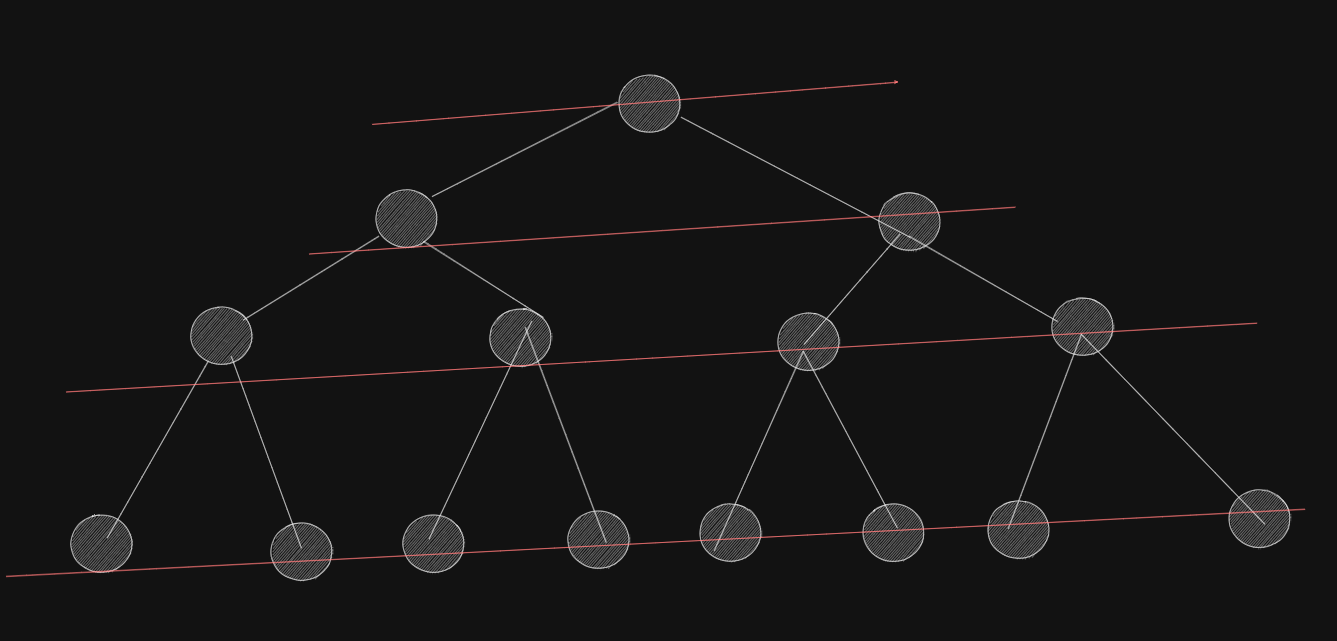
This is how BFS works
- Initialization: Begin by enqueueing the root node onto a queue data structure.
- Iteration: While the queue is not empty, perform the following steps:
- Dequeue and Visit: Dequeue the front node from the queue. Process the dequeued node (based on the problem’s requirements).
- Enqueue Children: Enqueue all child nodes of the dequeued node onto the queue (if any exist).
- Repeat: Continue steps 3 and 4 until the queue becomes empty. This ensures each level of the tree is processed before moving to the next level.
Depth First Search
DFS, inspired by how we explore mazes, delves deeply into paths before backtracking. It’s like systematically searching through a drawer’s items.
This method is effective for finding specific routes, searching, and understanding connections in structures. It can be done by either repeatedly exploring child paths using recursion, or by managing exploration steps manually with a stack.
By going deep first, DFS can uncover hidden solutions efficiently in complex situations.
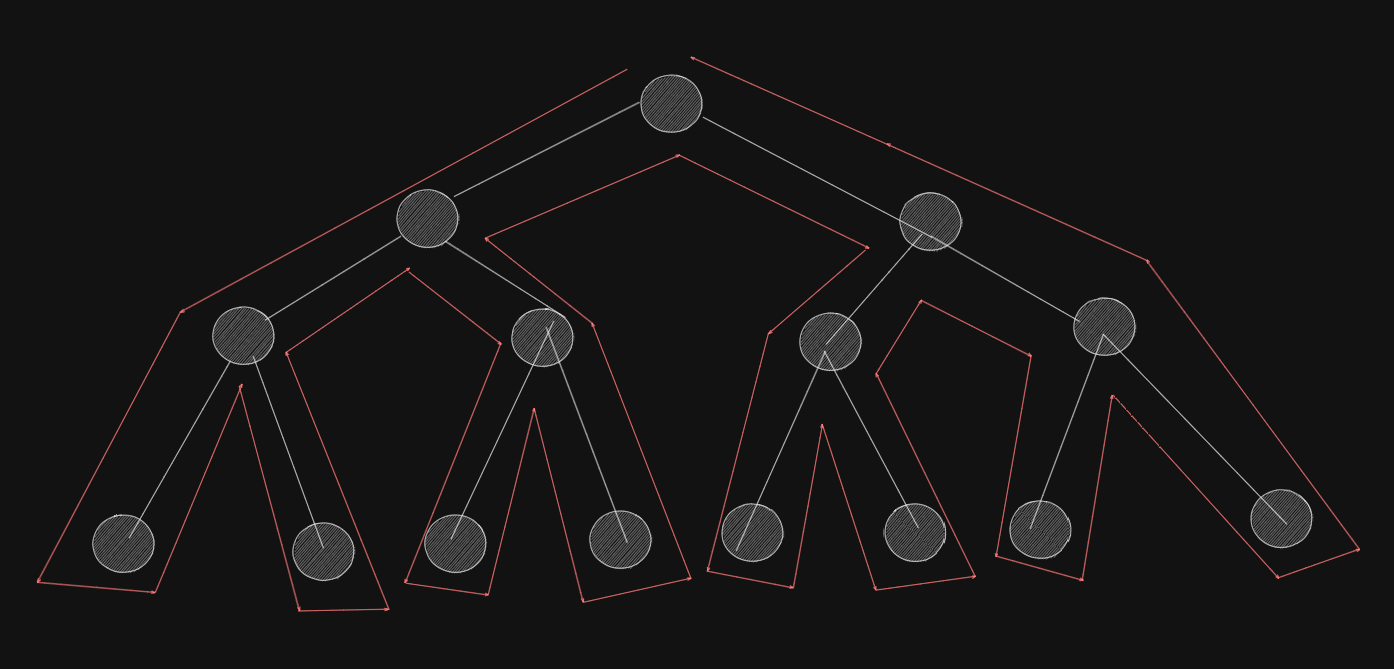
How DFS Works:
- Initialization: Start with the root node or starting point.
- Explore and Visit: Explore as deeply as possible along a branch before backtracking. Visit the current node (based on the problem’s requirements).
- Recursion or Stack: Use recursion or a stack to manage the traversal.
If using recursion, recursively apply the same process to the child nodes.
- Repeat: Continue steps 2 and 3 until all nodes are visited or the desired condition is met
Binary Search
Binary search is a clever algorithm used to find a specific value in a sorted list or array. It starts in the middle and checks if the desired value is higher or lower. Based on the result, it narrows down the search to the upper or lower half. This process continues until the target is found or the search range becomes empty.
This is how binary search works
- Initialization: Start with the entire sorted array or list and set two pointers, left and right, to the beginning and end respectively.
- Middle Element: Calculate the middle index between left and right. This is often done using the formula middle = (left + right) / 2.
- Comparison: Compare the value at the middle index with the target value you’re searching for.
- Three Possible Cases:
- If the middle value is equal to the target, you’ve found the value and the search is successful.
- If the middle value is less than the target, the target must be in the right half. Update left to middle + 1 to narrow the search to the right half.
- If the middle value is greater than the target, the target must be in the left half. Update right to middle – 1 to narrow the search to the left half.
- Repeat: Continue steps 2-4 until left becomes greater than right. This means the search range is empty, and the target value isn’t in the array.
Top K elements
This pattern helps us find the top, smallest, or frequently occurring ‘K’ elements from a given collection of items. The best data structure for keeping track of ‘K’ elements is a heap. Think of it like special storage that helps us manage these ‘K’ elements effectively.
Here is the minimal workflow of this approach
- Initial Population: Start by placing the first ‘K’ elements into the heap. Depending on the problem, you might use a min-heap or max-heap.
- Iterate and Update: Go through the remaining elements. If you find an element that’s larger (for a max-heap) or smaller (for a min-heap) than the heap’s top element, swap them.
- Maintaining K Elements: Keep the heap’s size limited to ‘K’. If it goes beyond ‘K’, remove the smallest (for max-heap) or largest (for min-heap) element from the heap.
Subsets
Many coding interview challenges involve working with different arrangements and selections of elements from a set. Starting with an empty set, we will iterate through all numbers one-by-one, and add them to existing sets to create subsets.
Let’s take a simple problem and understand how it works:
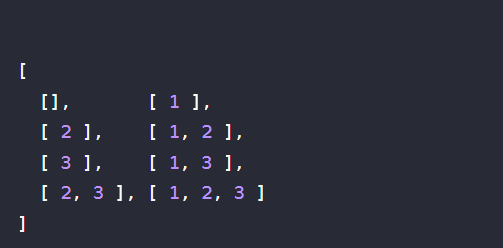
The question is from Leetcode: Given an integer array nums of unique elements, return all possible subsets. The solution set must not contain duplicate subsets. Return the solution in any order.
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
- We will start with an empty set: [ [ ] ]
- We will now add the first number to the set [ [] , [1] ]
- Now add the second number(2) to all the elements inside the set [2],[1,2]] and add it to the original set [ [], [1],[2],[1,2] ]
- Repeat the steps until all elements are traversed.
Here is a basic implementation of the above approach in JavaScript:
// Define a function called findallSubsets with a default array parameter sets.
function findallSubsets(sets = [1, 2, 3]) {
// Create an initial subset containing an empty array.
let subsets = [[]];
// Loop through each element in the sets array.
for (i = 0; i < sets.length; i++) {
// Get the current element.
let current = sets[i];
// Store the current number of subsets.
let lengthofSubset = subsets.length;
// Loop through existing subsets.
for (j = 0; j < lengthofSubset; j++) {
// Create a new subset by adding the current element to an existing subset.
// This creates a new subset for each existing subset.
subsets.push([…subsets[j], current]);
}
}
// Return the final array of subsets.
return subsets;
}
// Call the findallSubsets function without passing any arguments.
// By default, it will use [1, 2, 3] as the input set.
findallSubsets();
Output
While there are several other coding patterns that may be less frequently discussed compared to the aforementioned ones, if you’re interested in expanding your knowledge about these patterns, numerous free resources are available on the internet. These resources can provide you with further insights and guidance.
Wrapping it up
Thanks for taking the time to read about coding patterns for technical interviews. We’ve explored some really handy strategies that often come up during interviews.
From Two Pointers to Sliding Window, and from BFS to DFS, we’ve broken down these techniques to help you understand how they work. By getting the hang of these patterns, you’ll be ready to tackle various coding challenges in interviews with more confidence.
Good luck with your interview preparations!





Add comment