A guide to executing Linear Regression in Python

Regression and classification are two commonly used supervised learning algorithms and while classification is used for discrete values (e.g. email spam detection), regression is employed when the values are continuous (e.g. weather forecasting). Breaking down the term linear regression is important: ‘regression’ means that there is a causal or ‘cause and effect’ relationship between two or more variables and ‘linear’ implies that this correlation is linear, that is, if you plot it in a 2D space, you’d get a straight line. 

Linear regression has a wide range of real-life applications from assessing the risks that insurance providers take to vendors adjusting their prices based on income statistics. Modelling such data in Python is fairly easy too. In this guide you’ll learn some basic linear regression theory and how to execute linear regression in Python.

What is simple linear regression?

In linear regression, you map dependent variables with independent variables. The dependent features are also known as outputs or responses and the independent features are called inputs or predictors. Here is some theory based on insights from Mirko Stojiljković’s article on Real Python.

A linear regression model can be defined by the equation:

𝑦 = 𝛽₀ + 𝛽₁𝑥₁ + ⋯ + 𝛽_n𝑥_n + 𝜀

𝑦 is the dependent feature

x = (𝑥₁, … 𝑥_n) are the independent features 

𝛽₀…𝛽_n are the regression coefficients or model parameters

𝜀 is the error of estimation, which can be averaged out to be zero

In case of simple linear regression, there is only one independent feature.

So, the regression model narrows down to:

𝑦 = 𝛽₀ + 𝛽₁𝑥₁

In carrying out linear regression you are arriving at estimators for 𝛽₀…𝛽_n, the regression coefficients.

The estimated regression function then is:

𝑓(x) = 𝑏₀ + 𝑏₁𝑥₁ + ⋯ + 𝑏_n𝑥_n

At any given point, the difference between the actual and predicted response would be the residual (R).

For 𝑖 = 1, …, m,

      R_i = 𝑦_i – 𝑓(𝐱_ᵢ) 

To arrive at the best set of coefficients, the goal is to minimize the SSR, sum of squared residuals. 

SSR = Σᵢ(𝑦ᵢ – 𝑓(𝐱ᵢ))²

How to execute simple linear regression in Python?

To implement simple linear regression in Python you can use the machine learning package Scikit-Learn. You can try out the code on Jupyter.

Import libraries

Pick the dataset

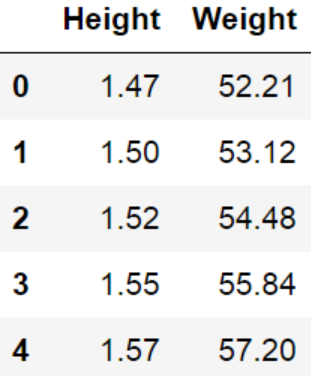
Consider this simple dataset provided by T McKetterick on Kaggle which provides, from a small sample of American women aged 30-39, average mass as a function of height.

Now, importing the CSV using pandas:

To get a glimpse of the dataset, execute:

The output is:

(15, 2)

And to view some of the data run:

The output is:

To “see” if the data would be good for linear regression, it makes sense to plot it.

The result is:

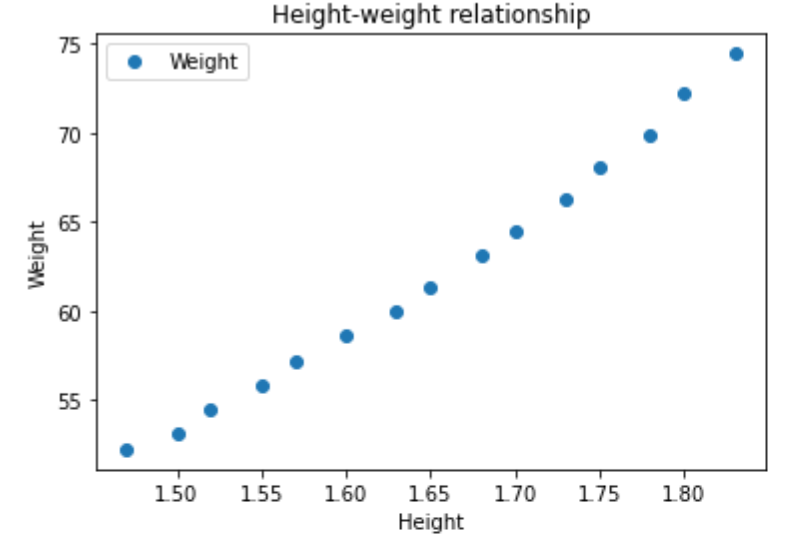
As you can see, this is very linear in form.

Provide the data

Here, you are to divide the data into independent and dependent variables:

Create a linear regression model:
Now, on to creating a linear regression model with Scikit-Learn and fitting it with the dataset.

To train the model use:

The output is:

LinearRegression()

To predict features run:

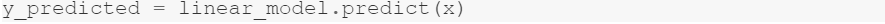
Evaluate the model

Root mean square error is a metric we want to minimise. So, let’s see how our model has performed:

View the results:

You get:
Root mean squared error: 0.49937056025884025
R2 score: 0.9891969224457968

Both these are very good values.

Also, take a look at the coefficients.

You get:

Slope: [61.27218654]
Intercept: -39.06195591884392

Having 𝑏₀ = -39 makes sense, as a person shouldn’t have positive weight for zero height (x).

Take a look at the line predicted by the model:

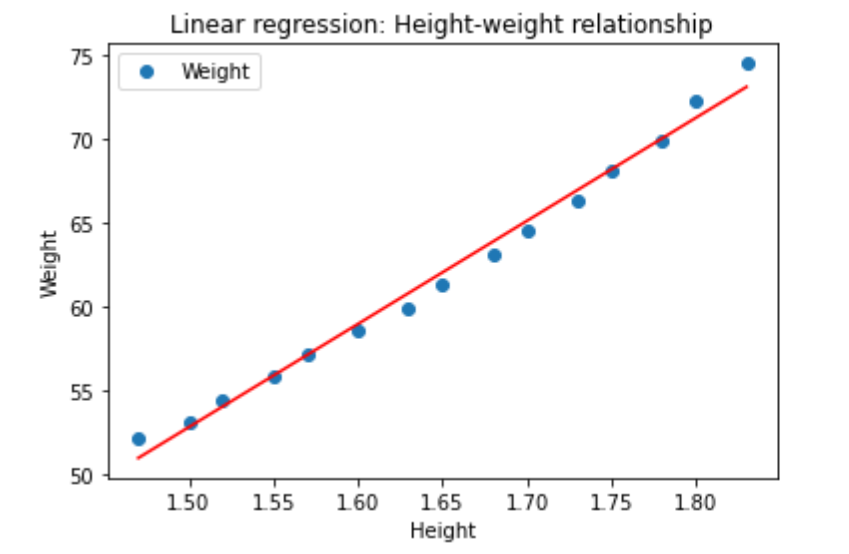
Now that you have a working model, you can use it to predict dependent variables for a new dataset, say, for a larger group of women of a similar age group and demographic.

So, you could get weight values for random heights, such as, 1.3, 1.5, 1.2, 2.4, 1:

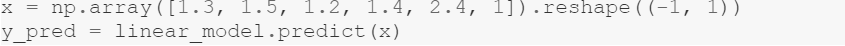
Have a look at x and y_pred:

You get:

[[1.3]
[1.5]
[1.2]
[1.4]
[2.4]
[1. ]]

And similarly,

To get:

[ 40.59188659 52.84632389 34.46466793 46.71910524 107.99129178
22.21023062]

How to execute multiple linear regression in Python?

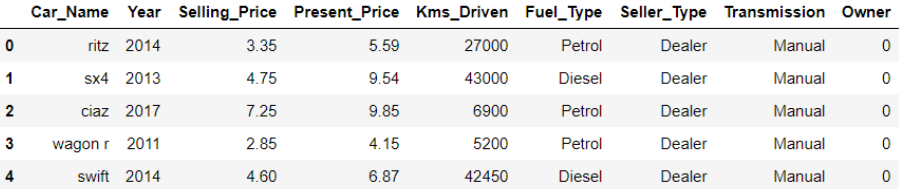
As an example of multiple linear regression consider data on cars from CarDekho, available at Kaggle.

Import Libraries

Provide the dataset

To view the first 5 rows of data:

You get:

Prepare the data
Now, for the purpose of evaluation, consider that the present price depends on only 3 of the above factors: years, selling price, and kilometers driven.

This time around, try dividing the dataset itself, into training and testing sets. You could keep a ratio of 80:20.

You can view the dimensions of the matrices:

You get:
(240, 3)
(61, 3)
(240,)
(61,)

Train and test

Once again, use Scikit-Learn library to train and test:

The output is:

LinearRegression()

In multiple linear regression, the model will try to arrive at optimal values for all coefficients.

You can view these now:

You get:

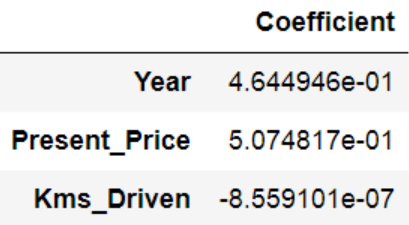
That is, if the present price increases by ‘1 unit’, the selling price should increase by 1.87 units. (e^-1 ~ 3.68). Or if the kilometers driven increase by 1 unit, the selling price drops by 3.14 units.

Prediction and evaluation
You can now make predictions on the dataset:

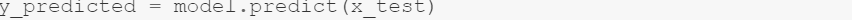
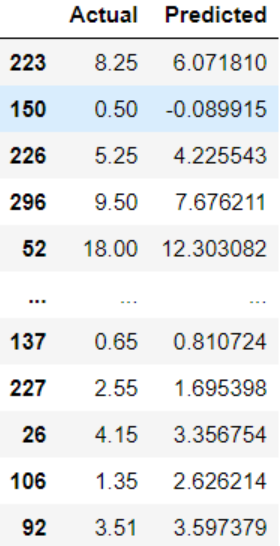
To view actual vs precited values,

This is what you get:

You can now evaluate RMSE and R2 score for training and test data:

You get,

RMSE = 2.040579021493682
R2 score = 0.8384238519780597

And for the test data:

You get:

RMSE = 1.6867312004140655
R2 score = 0.887446046362064

So, what do you think? 

1. Are these metrics a good starting point? 

2. Or would it help to carry out some exploratory analysis first, and have some other variables play a factor in deciding the selling price?

In the field of data science, being inquisitive helps arrive at the right answers. 

It also helps to work on projects with some of the best minds in the industry, and for that, you can simply sign up with Talent500. Our dynamic skill assessment algorithms align your skills to premium job openings at Fortune 500 companies. This way you’ll put what you learn in data science to practice and get hands-on experience with top real-world problems!

*You can gain complimentary insight from the following blogs, which also served as resource material for this post:

https://realpython.com/linear-regression-in-python/#polynomial-regression

https://stackabuse.com/linear-regression-in-python-with-scikit-learn/

https://towardsdatascience.com/linear-regression-on-boston-housing-dataset-f409b7e4a155